如图，四边形ABCD中，AD∥BC，AC与BD相交于点O，
（1）△ABC与△DBC的面积相等吗？为什么？
（2）若S△AOB=21cm2，求S△COD；
（3）若S△AOD=10cm2，且BO：OD=2：1，求S△ABD．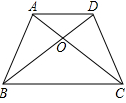
（1）根据已知得出∴△ABC的边BC上的高和△DBC边BC上的高相等，设此高为h，根据三角形的面积公式求出即可；
（2）根据△ABC的面积和△DBC的面积相等，都减去△OBC的面积，即可得出△AOB的面积和△DOC的面积相等；
（3）求出BD=3OD，根据面积公式代入求出即可．
解：（1））△ABC与△DBC的面积相等，理由是：
∵AD∥BC，
∴△ABC的边BC上的高和△DBC边BC上的高相等，设此高为h，
∴△ABC的面积是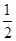
BC×h，△DBC的面积是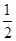×BC×h，
∵BC=BC，
∴△ABC与△DBC的面积相等；
（2）∵S△ABC=S△DBC，
∴S△ABC﹣S△OBC=S△DBC﹣S△OBC，
∴S△AOB=S△DOC=21cm2，
即S△COD=21cm2；
（3）∵BO：OD=2：1，
∴BD=3OD，
∵△AOD的边OD上的高和△ABD的边BD上的高相等，设此高为a，
∵S△AOD=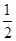×OD×a=10cm2，
∴S△ABD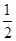．=×BD×a=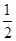×3OD×a=3×10cm2=30cm2．
【题目】
如图，AF是△ABC的高，AD是△ABC的角平分线，且∠B=38°，∠C=72°，求∠DAF的度数．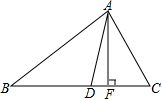
宏远商贸公司有A、B两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
| |
体积（m3／件） |
质量（吨／件） |
| A型商品 |
0.8 |
0.5 |
| B型商品 |
2 |
1 |
（1）已知一批商品有A、B两种型号，体积一共是20 m3 ,质量一共是10.5吨，直接写出A型号商品有 件；B两种型号商品有 件。
（2）物流公司现有可供使用的货车每辆额定载重3.5吨，容积为6 m3,其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元.
要将（1）中的商品一次或分批运输到目的地，宏远商贸公司应如何选择运送、付费方式运费最少?并求出该方式下的运费是多少元？
如图，坐标系上有A（2，0）、B（4，0）两点.二次函数
的图象经过这两点
（1）求这个二次函数的解析式；
（2）设该二次函数的图象的顶点为P，抛物线向上或向下平移多少个单位，则△ABP是正三角形。
据交管部门统计，高速公路超速行驶是引发交通事故的主要原因．我市某校数学课外小组的几个同学想尝试用自己所学的知识检测车速，甬台温高速公路温州—瑞安路段的限速是：每小时80千米（即最高时速不超过80千米），如图，他们将观测点设在离公路L的距离为0.1千米的P处．这时，一辆轿车由温州向瑞安匀速直线驶来，测得此车从A处行驶到B处所用的时间为3秒，并测得∠APO＝60°，∠BPO＝45°．试计算AB的长度并判断此车是否超速？
网格中每个小正方形的边长都是1.
（1）将图①中的格点三角形ABC平移，使点A平移至点A`，画出平移后的三角形；
（2）在图②中画一个格点三角形DEF，使△DEF∽△ABC，且相似比为2∶1；
（3）在图③中画一个格点三角形PQR，使△PQR∽△ABC，且相似比为
∶1.
（4）图②与图③中的△DEF与△PQR的相似比为
，试求出AD的长.
粤公网安备 44130202000953号