如图, ABCD中,点E、F在BD上,且BF=DE.
ABCD中,点E、F在BD上,且BF=DE.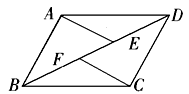
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
相关知识点
推荐套卷
如图, ABCD中,点E、F在BD上,且BF=DE.
ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.