如图，在平面直角坐标系中，抛物线
经过A（﹣1，0），B（3，0），C（0，3）三点，其顶点为D．连接BD，点P是线段BD上一个动点（不与B，D重合），过点P作y轴的垂线，垂足为E，连接BE．
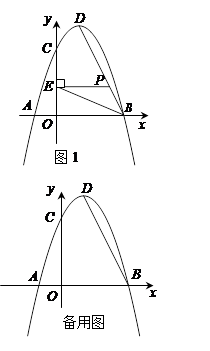
（1）求抛物线的解析式，并写出顶点D的坐标；
（2）如果点P的坐标为（x，y），△PBE的面积为S，求S与x的函数关系式，并求出S的最大值；
（3）在（2）的条件下，当S取得最大值时，过点P作x轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为P′，请求出点P′的坐标．
把下列各数的序号填入相应的横线上：
①-0．78，②5，③+
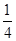，④8．47，⑤-10，⑥-
，⑦0，⑧
，⑨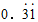
，⑩2．121121112…
整数有____________________________ ；（填序号）
分数有____________________________；（填序号）
有理数有___________________________；（填序号）
无理数有___________________________；（填序号）
如图，已知正方形ABCD中，边长为10cm，点E在AB边上，BE=6cm．如果点P在线段BC上以2cm/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动，设运动的时间为t秒，
①CP的长为 cm（用含t的代数式表示）；
②若点Q的运动速度与点P的运动速度相等，经过2秒后，△BPE与△CQP是否全等？请说明理由．
③若点Q的运动速度与点P的运动速度不相等，△BPE与△CQP能否全等，若能全等，求出点Q的运动速度，若不能全等，请说明理由．
两个大小不同的等腰直角三角形三角板按图1所示的位置放置，图2是由它抽象出的几何图形，AB=AC，AE=AD，∠BAC=∠EAD=90°，B，C，E在同一条直线上，连接DC．
（1）请找出图2中与△ABE全等的三角形，并给予证明；
（2）证明：DC⊥BE．
粤公网安备 44130202000953号