把下列各数的序号填入相应的横线上：
①-0．78，②5，③+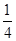
，④8．47，⑤-10，⑥-
，⑦0，⑧
，⑨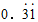
，⑩2．121121112…
整数有____________________________ ；（填序号）
分数有____________________________；（填序号）
有理数有___________________________；（填序号）
无理数有___________________________；（填序号）
相关试题
某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．
设每件商品的售价上涨 元（ 为正整数），每个月的销售利润为 元．
（1）求 与 的函数关系式并直接写出自变量的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
（3）为了使顾客尽量满意，每件商品的售价定为多少元时，每个月的利润恰为2200元？
先阅读，再回答问题：如果x1，x2是关于x的一元二次方程ax2＋bx＋c＝0（a≠0）的两个根，那么x1＋x2，x1x2与系数a，b，c的关系是：x1＋x2＝－
，x1x2＝
.例如：若x1，x2是方程2x2－x－1＝0的两个根，则x1＋x2＝－＝－
＝
，x1x2＝＝＝－．
若x1，x2是方程2x2＋x－3＝0的两个根，（1）求x1＋x2，x1x2
（2）求
＋
的值．
（3）求（x1－x2）2
经过点A（1,0），与y轴交于点B。
相关知识点
推荐套卷
粤公网安备 44130202000953号