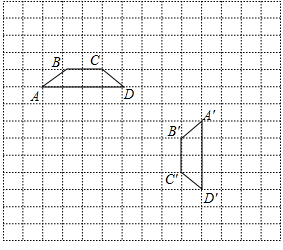在小正方形组成的15×15的网格中,四边形ABCD和四边形A′B′C′D′的位置如图所示.
(1)现把四边形ABCD绕D点按顺时针方向旋转90°,画出相应的图形A1B1C1D1,
(2)若四边形ABCD平移后,与四边形A′B′C′D′成轴对称,写出满足要求的一种平移方法,并画出平移后的图形A2B2C2D2.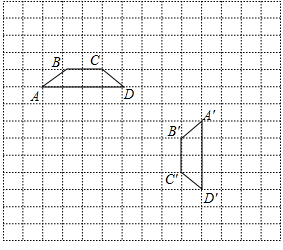
在小正方形组成的15×15的网格中,四边形ABCD和四边形A′B′C′D′的位置如图所示.
(1)现把四边形ABCD绕D点按顺时针方向旋转90°,画出相应的图形A1B1C1D1,
(2)若四边形ABCD平移后,与四边形A′B′C′D′成轴对称,写出满足要求的一种平移方法,并画出平移后的图形A2B2C2D2.