当今，青少年视力水平的下降已引起全社会的关注．为了解某校初中二年级300名学生的视力情况，从中随机抽查了一部分学生的视力，将其整理后，画出频数分布直方图，如图．
（1）随机抽查了_________ 名学生的视力；
（2）若视力在4.85以上属于正常，不需矫正，估计该校二年级300名学生中约有多少名学生的视力不需要矫正；
（3）若要使该校视力正常的百分率提高到70%，估计要有多少名学生通过矫正达到正常？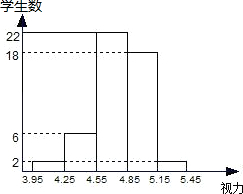
相关试题
当今，青少年视力水平的下降已引起全社会的关注．为了解某校初中二年级300名学生的视力情况，从中随机抽查了一部分学生的视力，将其整理后，画出频数分布直方图，如图．
（1）随机抽查了_________ 名学生的视力；
（2）若视力在4.85以上属于正常，不需矫正，估计该校二年级300名学生中约有多少名学生的视力不需要矫正；
（3）若要使该校视力正常的百分率提高到70%，估计要有多少名学生通过矫正达到正常？
即
即
等于多少？并写出推导过程。
（
）个等式。
中，点
是
边上一动点，过点
∥
，设
的平分线于点
，交
。
；
为怎样的四边形，并证明你的结论；
的一条对角线
平移
的位置，
是等腰三角形吗？为什么？
的对角线
的垂直平分线与边
，
分别交于点
，
，四边形
是否是菱形。
沿
，
同时折叠，
、
两点恰好都落在
边的
点处，若
，
，
，则长方形
粤公网安备 44130202000953号