(本小题满分12分)某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为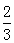 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为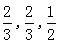 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ的分布列和数学期望;
(Ⅱ)用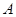 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用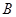 表示“甲队总得分大于乙队总得分” 这一事件,求
表示“甲队总得分大于乙队总得分” 这一事件,求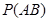 .
.
推荐套卷
(本小题满分12分)某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为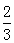 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为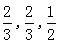 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ的分布列和数学期望;
(Ⅱ)用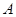 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用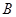 表示“甲队总得分大于乙队总得分” 这一事件,求
表示“甲队总得分大于乙队总得分” 这一事件,求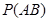 .
.