已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为
，两个焦点分别为
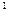和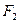
，椭圆G上一点到
和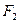的距离之和为12．
圆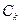
：
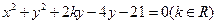的圆心为点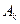
．
（1）求椭圆G的方程；（2）求
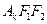面积；（3）问是否存在圆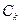包围椭圆G？请说明理由．
相关试题
在
处取得极值－2.
的解析式； 
在点
处的切线方程.
求证：
.
的单调区间;
上的最小值;
,
恒成立,求实数
的取值范围．
中，
，且
成等差数列，
成等比数列
.
；
推荐套卷
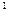已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为，两个焦点分别为和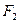，椭圆G上一点到和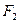的距离之和为12．
圆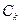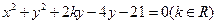：的圆心为点．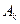
（1）求椭圆G的方程；（2）求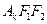面积；（3）问是否存在圆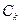包围椭圆G？请说明理由．
粤公网安备 44130202000953号