（满分14分）在斜四棱柱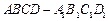
中，已知底面
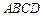是边长为4的菱形，
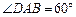，且点
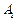在面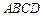上的射影是底面对角线
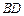与AC的交点O，设点E是
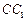的中点，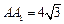
．
（Ⅰ） 求证：四边形
是矩形；
（Ⅱ） 求二面角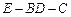
的大小；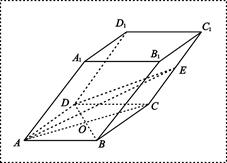
（Ⅲ） 求四面体
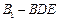的体积．
的最小值，使得存在以红点为顶点的
，
；
．
中，已知
，且
四点共圆．
四点共圆的充分必要条件是
．
的所有整数对
．
．推荐套卷
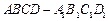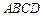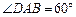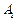（满分14分）在斜四棱柱中，已知底面是边长为4的菱形，，且点在面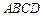上的射影是底面对角线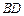与AC的交点O，设点E是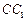的中点，．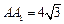
（Ⅰ） 求证：四边形是矩形；
（Ⅱ） 求二面角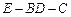的大小； （Ⅲ） 求四面体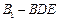的体积．
粤公网安备 44130202000953号