（文科）已知以原点为对称中心、F（2,0）为右焦点的椭圆C过点P（2，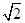
），直线
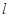：y=kx+m（k≠0）交椭圆C于不同的两点A、B。
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在k的值，使线段AB的垂直平分线经过点Q（0,3），若存在求出 k的取值范围，若不存在，请说明理由。
相关试题
，对任意
，恒有
。求：
，
，
的值；
在
上的最值。
时，
。当
时，
，又
，写出
的表达式并作出其图象。
是幂函数，且当
时为减函数，
奇偶性并说明理由。
，
，求
。
的定义域为
，且对任意
，都有
，当
时，
恒成立．推荐套卷
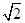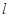（文科）已知以原点为对称中心、F（2,0）为右焦点的椭圆C过点P（2，），直线：y=kx+m（k≠0）交椭圆C于不同的两点A、B。
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在k的值，使线段AB的垂直平分线经过点Q（0,3），若存在求出 k的取值范围，若不存在，请说明理由。
粤公网安备 44130202000953号