(文科)已知中心在原点的双曲线C的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以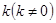 为斜率的直线
为斜率的直线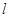 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求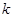 的取值范围.
的取值范围.
推荐套卷
(文科)已知中心在原点的双曲线C的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以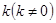 为斜率的直线
为斜率的直线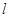 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求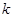 的取值范围.
的取值范围.