（文科）如图，椭圆E：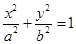
（a＞b＞0）的左焦点为F1，右焦点为F2，离心率
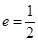．过F1的直线交椭圆于A、B两点，且△ABF2的周长为8．
（1）求椭圆E的方程；
（2）设动直线l：y＝kx＋m与椭圆E有且只有一个公共点P，且与直线x＝4相交于点Q．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．
相关试题
和
，且
.
，
的表达式；
时，不等式
在
上恒成立，求实数
的取值范围.
和
．其中
．
与
的图像的一个公共点恰好在
轴上，求
的值；
和
是方程
的两根，且满足
，证明：当
时，
．
.
时，求曲线
在点
处的切线方程；
，且
，求函数
的单调区间.
的函数
（
为实数）。
是奇函数，求
都有
成立.
中，内角
的对边分别为
，并且
.
的大小；
，求
.推荐套卷
（文科）如图，椭圆E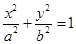：（a＞b＞0）的左焦点为F1，右焦点为F2，离心率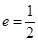．过F1的直线交椭圆于A、B两点，且△ABF2的周长为8．
（1）求椭圆E的方程；
（2）设动直线l：y＝kx＋m与椭圆E有且只有一个公共点P，且与直线x＝4相交于点Q．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．
粤公网安备 44130202000953号