(文科)已知椭圆 的左、右两个顶点分别为A,B,直线
的左、右两个顶点分别为A,B,直线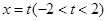 与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
(1)求证:无论t如何变化,圆C1与圆C2的圆心距是定值;
(2)当t变化时,求圆C1与圆C2的面积的和S的最小值.
推荐套卷
(文科)已知椭圆 的左、右两个顶点分别为A,B,直线
的左、右两个顶点分别为A,B,直线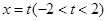 与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
与椭圆相交于M,N两点,经过三点A,M,N的圆与经过三点B,M,N的圆分别记为圆C1与圆C2.
(1)求证:无论t如何变化,圆C1与圆C2的圆心距是定值;
(2)当t变化时,求圆C1与圆C2的面积的和S的最小值.