【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
【探究展示】
（1）证明：AM=AD+MC；
（2）AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．
【拓展延伸】
（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．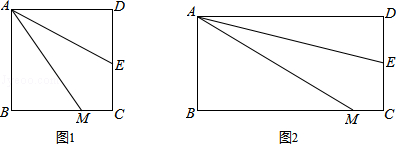
相关试题
【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
【探究展示】
（1）证明：AM=AD+MC；
（2）AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．
【拓展延伸】
（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．
多800元，一、二、三年级捐款数是四、五、六年级捐款数的
全校共捐款多少元？
粤公网安备 44130202000953号