己知四棱锥P-ABCD，其中底面ABCD为矩形，侧棱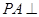
底面ABCD，其中BC=2AB=2PA=6，
M,N为侧棱PC上的两个三等分点，如图所示：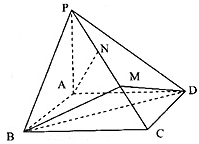
（1）求证： AN∥平面MBD；
（2）求锐二面角B-PC-A的余弦值．
中，已知
，
.
(Ⅰ)求
的值
；
为
的中点，求
的长
的前100项
的和。
满足
，且
.
是等差数列，并求通项
； 
的值；
的首项
，公差
．且
分别是等比数列
的
． 
对任意自然数
均有：
成立．求
的值。
的三内角A，B，C所对三边分别为a，b，c，且
的值。
求a的值。相关知识点
推荐套卷
己知四棱锥P-ABCD，其中底面ABCD为矩形，侧棱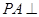底面ABCD，其中BC=2AB=2PA=6，
M,N为侧棱PC上的两个三等分点，如图所示：
（1）求证： AN∥平面MBD；
（2）求锐二面角B-PC-A的余弦值．
粤公网安备 44130202000953号