(本小题满分14分)如图,椭圆 和圆
和圆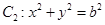 ,已知椭圆
,已知椭圆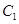 过点
过点 ,焦距为2.
,焦距为2.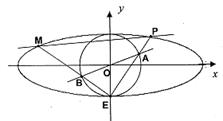
(1)求椭圆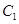 的方程;
的方程;
(2)椭圆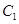 的下顶点为
的下顶点为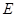 ,过坐标原点
,过坐标原点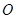 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线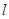 与圆
与圆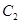 相交于点
相交于点 ,直线
,直线 与椭圆
与椭圆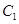 的另一个交点分别是点
的另一个交点分别是点 .设
.设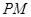 的斜率为
的斜率为 ,直线
,直线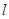 斜率为
斜率为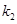 ,求
,求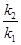 的值.
的值.
推荐套卷
(本小题满分14分)如图,椭圆 和圆
和圆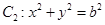 ,已知椭圆
,已知椭圆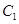 过点
过点 ,焦距为2.
,焦距为2.
(1)求椭圆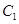 的方程;
的方程;
(2)椭圆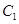 的下顶点为
的下顶点为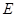 ,过坐标原点
,过坐标原点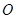 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线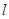 与圆
与圆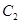 相交于点
相交于点 ,直线
,直线 与椭圆
与椭圆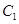 的另一个交点分别是点
的另一个交点分别是点 .设
.设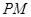 的斜率为
的斜率为 ,直线
,直线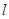 斜率为
斜率为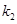 ,求
,求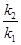 的值.
的值.