如图,某商业中心O有通往正东方向和北偏东30º方向的两条街道,某公园P位于商业中心北偏东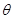 角(
角(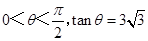 ),且与商业中心O的距离为
),且与商业中心O的距离为 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
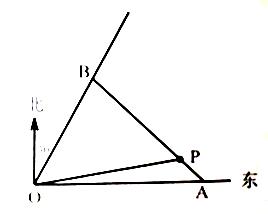
(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
推荐套卷
如图,某商业中心O有通往正东方向和北偏东30º方向的两条街道,某公园P位于商业中心北偏东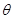 角(
角(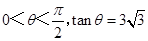 ),且与商业中心O的距离为
),且与商业中心O的距离为 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。

(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。