如图,我市有一个健身公园,由一个直径为2km的半圆和一个以 为斜边的等腰直角三角形
为斜边的等腰直角三角形 构成,其中
构成,其中 为
为 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道 ,按实际需要,四边形
,按实际需要,四边形 的两个顶点
的两个顶点 分别在线段
分别在线段 上,另外两个顶点
上,另外两个顶点 在半圆上,
在半圆上, 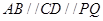 ,且
,且 间的距离为1km.设四边形
间的距离为1km.设四边形 的周长为
的周长为 km.
km.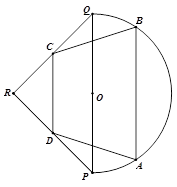
(1)若 分别为
分别为 的中点,求
的中点,求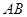 长;
长;
(2)求周长 的最大值.
的最大值.
推荐套卷
如图,我市有一个健身公园,由一个直径为2km的半圆和一个以 为斜边的等腰直角三角形
为斜边的等腰直角三角形 构成,其中
构成,其中 为
为 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道 ,按实际需要,四边形
,按实际需要,四边形 的两个顶点
的两个顶点 分别在线段
分别在线段 上,另外两个顶点
上,另外两个顶点 在半圆上,
在半圆上, 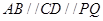 ,且
,且 间的距离为1km.设四边形
间的距离为1km.设四边形 的周长为
的周长为 km.
km.
(1)若 分别为
分别为 的中点,求
的中点,求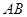 长;
长;
(2)求周长 的最大值.
的最大值.