（本小题满分13分）我国东部某风景区内住着一个少数民族部落，该部落拟投资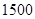
万元用于修复和加强民俗文化基础设施．据测算，修复好部落民俗文化基础设施后，任何一个月（每月均按
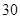天计算）中第
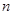天的游客人数
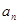近似满足
（单位：千人），第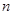天游客人均消费金额
近似满足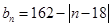
（单位：元）．
（1）求该部落第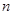天的日旅游收入
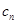（单位：千元，
，
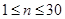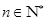）的表达式；
（2）若以一个月中最低日旅游收入金额的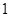
%作为每一天应回收的投资成本，试问该部落至少经过几年就可以收回全部投资成本．
（2）
（3）
与直线
及
所围成图形的面积.
做直线运动，式中
为时间t内通过的距离，媒质的阻力与速度的平方成正比（比例常数为
），试求物体由
运动到
时，阻力所做的功.
的正三角形的厚纸，从这块厚纸的三个角，按右图那样切下三个全等的四边形后，做成一个无盖的盒子，要使这个盒子容积最大，
值应为多少？推荐套卷
（本小题满分13分）我国东部某风景区内住着一个少数民族部落，该部落拟投资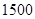万元用于修复和加强民俗文化基础设施．据测算，修复好部落民俗文化基础设施后，任何一个月（每月均按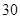天计算）中第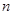天的游客人数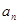近似满足（单位：千人），第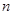天游客人均消费金额近似满足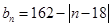（单位：元）．
（1）求该部落第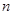天的日旅游收入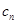（单位：千元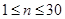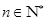，，）的表达式；
（2）若以一个月中最低日旅游收入金额的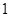%作为每一天应回收的投资成本，试问该部落至少经过几年就可以收回全部投资成本．
粤公网安备 44130202000953号