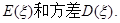某居民小区有两个相互独立的安全防范系统(简称系统)甲和乙,系统甲和系统乙在任意时刻发生故障的概率分别为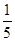 和
和 ,若在任意时刻至多有一个系统发生故障的概率为
,若在任意时刻至多有一个系统发生故障的概率为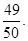
(Ⅰ)求 的值;
的值;
(Ⅱ)设系统乙在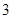 次相互独立的检测中不发生故障的次数为随机变量
次相互独立的检测中不发生故障的次数为随机变量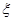 ,求
,求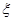 的数学期望
的数学期望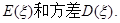
推荐套卷
某居民小区有两个相互独立的安全防范系统(简称系统)甲和乙,系统甲和系统乙在任意时刻发生故障的概率分别为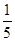 和
和 ,若在任意时刻至多有一个系统发生故障的概率为
,若在任意时刻至多有一个系统发生故障的概率为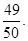
(Ⅰ)求 的值;
的值;
(Ⅱ)设系统乙在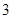 次相互独立的检测中不发生故障的次数为随机变量
次相互独立的检测中不发生故障的次数为随机变量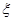 ,求
,求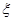 的数学期望
的数学期望