(本小题满分13分)等差数列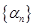 的前
的前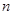 项和
项和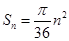 ,数列
,数列 满足
满足 .同学甲在研究性学习中发现以下六个等式均成立:
.同学甲在研究性学习中发现以下六个等式均成立:
①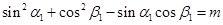 ;
;
② ;
;
③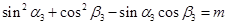 ;
;
④ ;
;
⑤ ;
;
⑥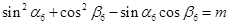 .
.
(1)求数列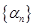 的通项公式,并从上述六个等式中选择一个,求实数
的通项公式,并从上述六个等式中选择一个,求实数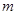 的值;
的值;
(2)根据(1)计算结果,将同学甲的发现推广为关于任意角 的三角恒等式,并证明你的结论.
的三角恒等式,并证明你的结论.
相关知识点
推荐套卷
(本小题满分13分)等差数列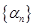 的前
的前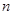 项和
项和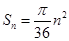 ,数列
,数列 满足
满足 .同学甲在研究性学习中发现以下六个等式均成立:
.同学甲在研究性学习中发现以下六个等式均成立:
①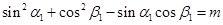 ;
;
② ;
;
③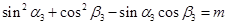 ;
;
④ ;
;
⑤ ;
;
⑥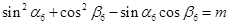 .
.
(1)求数列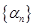 的通项公式,并从上述六个等式中选择一个,求实数
的通项公式,并从上述六个等式中选择一个,求实数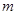 的值;
的值;
(2)根据(1)计算结果,将同学甲的发现推广为关于任意角 的三角恒等式,并证明你的结论.
的三角恒等式,并证明你的结论.