(本小题满分14分)
如右图，PA⊥平面ABCD，ABCD是矩形，PA=AB=1，∠PDA=30°，点F是PB的中点，
点E在边BC上，
（Ⅰ）若E为BC中点，证明：EF∥平面PAC；
（Ⅱ）证明：AF⊥平面PBC；
（Ⅲ）当BE等于何值时,二面角P—DE—A的大小为45°？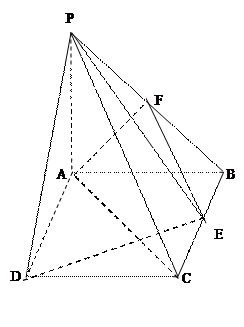
推荐套卷
(本小题满分14分)
如右图，PA⊥平面ABCD，ABCD是矩形，PA=AB=1，∠PDA=30°，点F是PB的中点，
点E在边BC上，
（Ⅰ）若E为BC中点，证明：EF∥平面PAC；
（Ⅱ）证明：AF⊥平面PBC；
（Ⅲ）当BE等于何值时,二面角P—DE—A的大小为45°？
粤公网安备 44130202000953号