本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
(理)对于曲线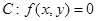 ,若存在最小的非负实数
,若存在最小的非负实数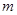 和
和 ,使得曲线
,使得曲线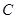 上任意一点
上任意一点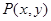 ,
,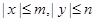 恒成立,则称曲线
恒成立,则称曲线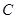 为有界曲线,且称点集
为有界曲线,且称点集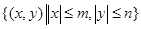 为曲线
为曲线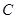 的界域.
的界域.
(1)写出曲线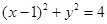 的界域;
的界域;
(2)已知曲线 上任意一点
上任意一点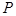 到坐标原点
到坐标原点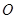 与直线
与直线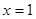 的距离之和等于3,曲线
的距离之和等于3,曲线 是否为有界曲线,若是,求出其界域,若不是,请说明理由;
是否为有界曲线,若是,求出其界域,若不是,请说明理由;
(3)已知曲线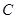 上任意一点
上任意一点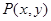 到定点
到定点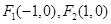 的距离之积为常数
的距离之积为常数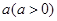 ,求曲线的界域.
,求曲线的界域.
相关知识点
推荐套卷
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
(理)对于曲线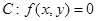 ,若存在最小的非负实数
,若存在最小的非负实数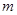 和
和 ,使得曲线
,使得曲线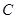 上任意一点
上任意一点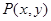 ,
,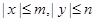 恒成立,则称曲线
恒成立,则称曲线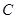 为有界曲线,且称点集
为有界曲线,且称点集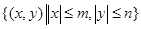 为曲线
为曲线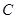 的界域.
的界域.
(1)写出曲线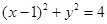 的界域;
的界域;
(2)已知曲线 上任意一点
上任意一点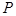 到坐标原点
到坐标原点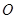 与直线
与直线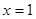 的距离之和等于3,曲线
的距离之和等于3,曲线 是否为有界曲线,若是,求出其界域,若不是,请说明理由;
是否为有界曲线,若是,求出其界域,若不是,请说明理由;
(3)已知曲线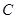 上任意一点
上任意一点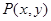 到定点
到定点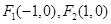 的距离之积为常数
的距离之积为常数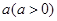 ,求曲线的界域.
,求曲线的界域.