设函数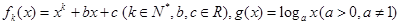 .
.
(1)若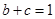 ,且
,且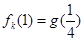 ,求
,求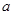 的值;
的值;
(2)若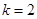 ,记函数
,记函数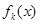 在
在 上的最大值为
上的最大值为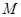 ,最小值为
,最小值为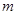 ,求
,求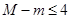 时的
时的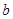 的取值范围;
的取值范围;
(3)判断是否存在大于1的实数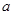 ,使得对任意
,使得对任意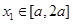 ,都有
,都有 满足等式:
满足等式: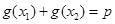 ,且满足该等式的常数
,且满足该等式的常数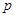 的取值唯一?若存在,求出所有符合条件的
的取值唯一?若存在,求出所有符合条件的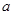 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
推荐套卷
设函数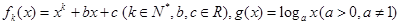 .
.
(1)若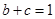 ,且
,且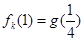 ,求
,求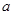 的值;
的值;
(2)若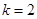 ,记函数
,记函数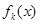 在
在 上的最大值为
上的最大值为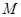 ,最小值为
,最小值为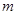 ,求
,求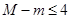 时的
时的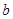 的取值范围;
的取值范围;
(3)判断是否存在大于1的实数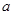 ,使得对任意
,使得对任意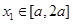 ,都有
,都有 满足等式:
满足等式: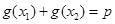 ,且满足该等式的常数
,且满足该等式的常数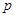 的取值唯一?若存在,求出所有符合条件的
的取值唯一?若存在,求出所有符合条件的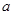 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.