(1)求与向量a=(2,-1,2)共线且满足方程a·x=-18的向量x的坐标;
(2)已知A、B、C三点坐标分别为(2,-1,2),(4,5,-1),(-2,2,3),求点P的坐标使得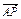 =
=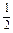 (
(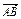 -
- );
);
(3)已知a=(3,5,-4),b=(2,1,8),求:①a·b;②a与b夹角的余弦值;
③确定 ,
, 的值使得
的值使得 a+
a+ b与z轴垂直,且(
b与z轴垂直,且( a+
a+ b)·(a+b)=53.
b)·(a+b)=53.
推荐套卷
(1)求与向量a=(2,-1,2)共线且满足方程a·x=-18的向量x的坐标;
(2)已知A、B、C三点坐标分别为(2,-1,2),(4,5,-1),(-2,2,3),求点P的坐标使得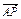 =
=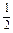 (
(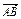 -
- );
);
(3)已知a=(3,5,-4),b=(2,1,8),求:①a·b;②a与b夹角的余弦值;
③确定 ,
, 的值使得
的值使得 a+
a+ b与z轴垂直,且(
b与z轴垂直,且( a+
a+ b)·(a+b)=53.
b)·(a+b)=53.