某水域一艘装载浓硫酸的货船发生侧翻,导致浓硫酸泄漏,对河水造成了污染.为减少对环境的影响,环保部门迅速反应,及时向污染河道投入固体碱,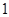 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度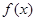 与时间
与时间 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: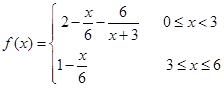 ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用.
(Ⅰ) 如果只投放1个单位的固体碱,则能够维持有效的抑制作用的时间有多长?
(Ⅱ) 第一次投放1单位固体碱后,当污染河道水中的碱浓度减少到 时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为
时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为 ,求
,求 的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)