如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.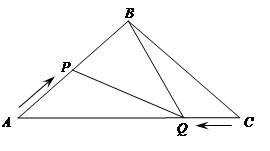
(1)当x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB,若存在,求出此时AP的长;若不存在,请说理由;
(3)当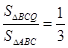 时,求
时,求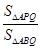 的值.
的值.
相关知识点
推荐套卷
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.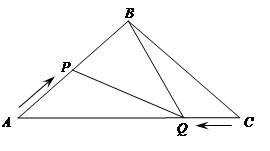
(1)当x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB,若存在,求出此时AP的长;若不存在,请说理由;
(3)当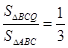 时,求
时,求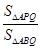 的值.
的值.