在△ABC中,∠A=30°,AB=2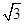 ,将△ABC绕点B顺时针旋转
,将△ABC绕点B顺时针旋转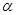 (0°<
(0°<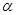 <90°),得到△DBE,其中点A的对应点是点D,点C的对应点是点E,AC、DE相交于点F,连接BF.
<90°),得到△DBE,其中点A的对应点是点D,点C的对应点是点E,AC、DE相交于点F,连接BF.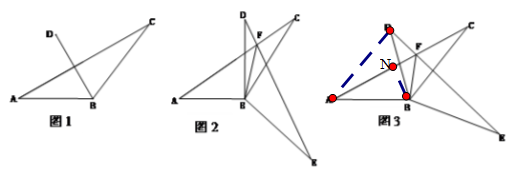
(1)如图1,若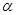 =60°,线段BA绕点B旋转
=60°,线段BA绕点B旋转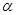 得到线段BD.请补全△DBE,并直接写出∠AFB的度数;
得到线段BD.请补全△DBE,并直接写出∠AFB的度数;
(2)如图2,若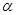 =90°,求∠AFB的度数和BF的长;
=90°,求∠AFB的度数和BF的长;
(3)如图3,若旋转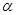 (0°<
(0°<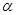 <90°),请直接写出∠AFB的度数及BF的长(用含
<90°),请直接写出∠AFB的度数及BF的长(用含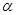 的代数式表示).
的代数式表示).
相关知识点
推荐套卷




 x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?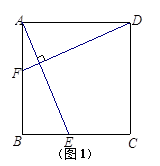
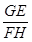 的值.
的值. 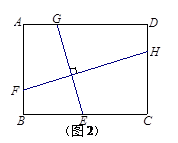
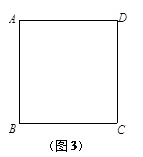
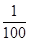 x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳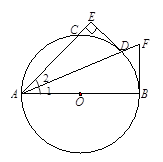
 粤公网安备 44130202000953号
粤公网安备 44130202000953号