某校七年级为拓宽学生的知识面，发展学生的兴趣爱好，开设了美术、书法、摄影、篮球等校本课程．下面是根据该校708班参加各种课程的人数绘制的两幅统计图．请你根据图中提供的信息回答下列问题：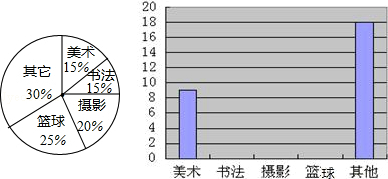
（1）该班共有多少学生；
（2）求出表示“其他”课程参加人数的扇形的圆心角的度数；
（3）补全条形统计图．
相关试题
的值与7－
的值相等.
的值，其中x=－2，y=2.
(2)、4(x－1)-3(20－x)=5(x－2)
(4)、
已知：甲、乙两车分别从相距300千米的A、B两地同时出发相向而行，甲到B地后立即返回，下图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．
（1）请直接写出甲、乙两车离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数关系式，并标明自变量x的取值范围；
（2）它们在行驶的过程中有几次相遇？并求出每次相遇的时间．
；
粤公网安备 44130202000953号