(本小题满分8分)如图,正方形网格中的每个小正方形边长都是1.
(利用网格线进行画图,别忘了标上字母噢!)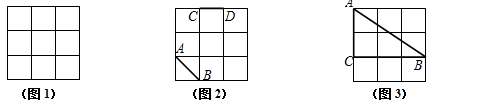
(1) 在图1中,画一个顶点为格点、面积为5的正方形;
(2) 在图2中,已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;
(要求画出所有符合题意的线段)
(3) 在图3中,找一格点D,满足:①到CB、CA的距离相等;②到点A、C的距离相等.
相关知识点
推荐套卷
(本小题满分8分)如图,正方形网格中的每个小正方形边长都是1.
(利用网格线进行画图,别忘了标上字母噢!)
(1) 在图1中,画一个顶点为格点、面积为5的正方形;
(2) 在图2中,已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;
(要求画出所有符合题意的线段)
(3) 在图3中,找一格点D,满足:①到CB、CA的距离相等;②到点A、C的距离相等.