如图,已知AB是⊙O的直径,AB=8,点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.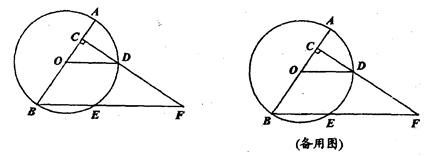
(1)若ED=BE,求∠F的度数:
(2)设线段OC=a,求线段BE和EF的长(用含a的代数式表示);
(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.
相关知识点
推荐套卷
如图,已知AB是⊙O的直径,AB=8,点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.
(1)若ED=BE,求∠F的度数:
(2)设线段OC=a,求线段BE和EF的长(用含a的代数式表示);
(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.