(本题10分)元旦期间,七(1)班的小明、小丽等同学随家长一行共12人同到某公园游玩,小明爸爸根据贴在公园门口的下表购买了成人票和学生票共花去350元。
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明爸爸想一想,购买门票有更省钱的方式吗?如果有,怎么买?说明理由。
| |
成人票 |
学生票 |
团体票(16人以上含16人) |
| 票价 |
35元/ 张 |
17.5元/ 张 |
21元/ 张 |
相关知识点
推荐套卷
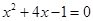 (配方法)(2)
(配方法)(2)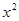 -4x-12=0(公式法)
-4x-12=0(公式法)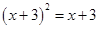 .(4)
.(4)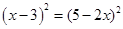
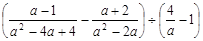 ,其中
,其中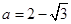
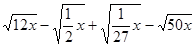 (2)
(2)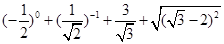
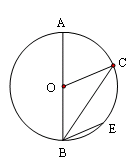
 中,Rt△OAB和Rt△OCD的直角顶点A,C始终在
中,Rt△OAB和Rt△OCD的直角顶点A,C始终在 轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为
轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为 .试解决下列问题:
.试解决下列问题: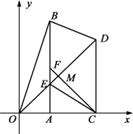
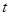 ,请把BD长表示成关于
,请把BD长表示成关于 粤公网安备 44130202000953号
粤公网安备 44130202000953号