“爆竹声声一岁除”,除夕和春节期间燃放爆竹是中国人的传统风俗习惯,但这种习惯会造成空气污染,为了了解某市市民春节期间购买、燃放烟花爆竹的原因,该市统计局随机调查了该市部分15周岁以上常住市民,对调查结果整理后,绘制如图尚不完整的统计图表.
组别
|
原因
|
人数
|
A
|
不想改变传统风俗习惯
|
650
|
B
|
增添节日喜庆气氛
|
300
|
C
|
祈福运、求吉利、辟邪害
|
m
|
D
|
没有可替代的庆祝方式
|
150
|
E
|
为了孩子的玩耍和快乐
|
n
|
F
|
其他
|
100
|
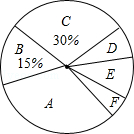
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中D组所占的百分比为 .
(2)若该市人口约为800万,请你估计其中属于B组的市民有多少人?(用科学记数法表示);
(3)若在此次接受调查的市民中随机抽取一人,此人属于A组的概率是多少?