(本小题满分14分)给定正奇数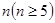 ,数列
,数列 :
: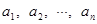 是1,2,…,
是1,2,…,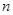 的一个排列,定义E(
的一个排列,定义E(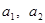 ,…,
,…,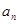 )
)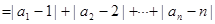 为数列
为数列 :
: ,
,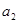 ,…,
,…,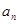 的位差和.
的位差和.
(1)当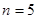 时,求数列
时,求数列 :1,3,4,2,5的位差和;
:1,3,4,2,5的位差和;
(2)若位差和E( ,
,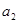 ,…,
,…,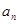 )=4,求满足条件的数列
)=4,求满足条件的数列 :
: ,
,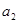 ,…,
,…,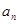 的个数;
的个数;
(3)若位差和 ,求满足条件的数列
,求满足条件的数列 :
: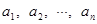 的个数.
的个数.
推荐套卷
(本小题满分14分)给定正奇数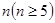 ,数列
,数列 :
: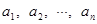 是1,2,…,
是1,2,…,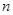 的一个排列,定义E(
的一个排列,定义E(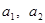 ,…,
,…,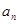 )
)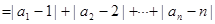 为数列
为数列 :
: ,
,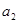 ,…,
,…,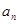 的位差和.
的位差和.
(1)当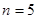 时,求数列
时,求数列 :1,3,4,2,5的位差和;
:1,3,4,2,5的位差和;
(2)若位差和E( ,
,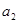 ,…,
,…,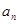 )=4,求满足条件的数列
)=4,求满足条件的数列 :
: ,
,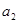 ,…,
,…,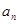 的个数;
的个数;
(3)若位差和 ,求满足条件的数列
,求满足条件的数列 :
: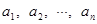 的个数.
的个数.