某班级共派出 个男生和
个男生和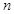 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有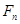 种选法.
种选法.
(1)试求 和
和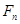 ;
;
(2)判断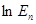 和
和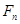 的大小(
的大小(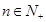 ),并用数学归纳法证明.
),并用数学归纳法证明.
相关知识点
推荐套卷
某班级共派出 个男生和
个男生和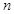 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有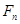 种选法.
种选法.
(1)试求 和
和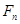 ;
;
(2)判断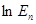 和
和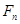 的大小(
的大小(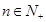 ),并用数学归纳法证明.
),并用数学归纳法证明.