(Ⅰ)求直线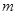 :
: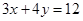 与两坐标轴所围成的三角形的内切圆
与两坐标轴所围成的三角形的内切圆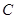 的方程;
的方程;
(Ⅱ)若与(Ⅰ)中的圆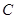 相切的直线
相切的直线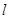 交
交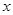 轴
轴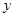 轴于
轴于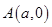 和
和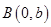 两点,且
两点,且 .
.
①求证:圆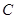 与直线
与直线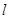 相切的条件为
相切的条件为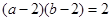 ;
;
②求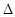 OAB面积的最小值及此时直线
OAB面积的最小值及此时直线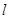 的方程.
的方程.
相关知识点
推荐套卷
(Ⅰ)求直线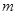 :
: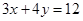 与两坐标轴所围成的三角形的内切圆
与两坐标轴所围成的三角形的内切圆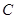 的方程;
的方程;
(Ⅱ)若与(Ⅰ)中的圆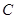 相切的直线
相切的直线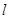 交
交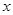 轴
轴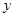 轴于
轴于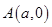 和
和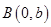 两点,且
两点,且 .
.
①求证:圆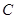 与直线
与直线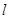 相切的条件为
相切的条件为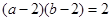 ;
;
②求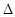 OAB面积的最小值及此时直线
OAB面积的最小值及此时直线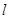 的方程.
的方程.