20. 集合A是由具备下列性质的函数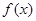 组成的:
组成的:
(1)函数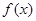 的定义域是
的定义域是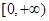 ;
;
(2)函数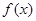 的值域是
的值域是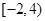 ;
;
(3)函数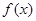 在
在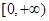 上是增函数.试分别探究下列两小题:
上是增函数.试分别探究下列两小题:
(Ⅰ)判断函数 ,及
,及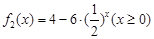 是否属于集合A?并证明.
是否属于集合A?并证明.
(Ⅱ)对于(Ⅰ)中你认为属于集合A的函数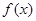 ,不等式
,不等式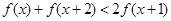 是否对于任意的
是否对于任意的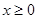 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.
推荐套卷
20. 集合A是由具备下列性质的函数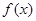 组成的:
组成的:
(1)函数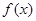 的定义域是
的定义域是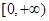 ;
;
(2)函数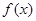 的值域是
的值域是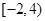 ;
;
(3)函数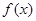 在
在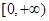 上是增函数.试分别探究下列两小题:
上是增函数.试分别探究下列两小题:
(Ⅰ)判断函数 ,及
,及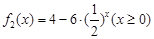 是否属于集合A?并证明.
是否属于集合A?并证明.
(Ⅱ)对于(Ⅰ)中你认为属于集合A的函数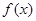 ,不等式
,不等式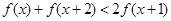 是否对于任意的
是否对于任意的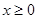 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.