(本小题满分8分)某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,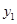 为方案一的函数图像,
为方案一的函数图像,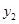 为方案二的函数图像.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
为方案二的函数图像.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):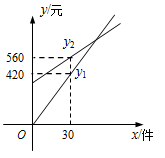
(1)求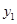 的函数解析式;
的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)小丽应选择哪种销售方案,才能使月工资更多?
相关知识点
推荐套卷
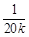 x+b,其中整数k使式子
x+b,其中整数k使式子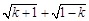 有意义.经测算,销售单价为60元时,年销售量为50000件.
有意义.经测算,销售单价为60元时,年销售量为50000件.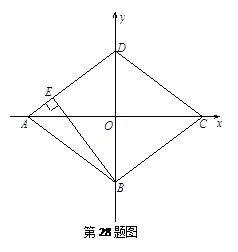

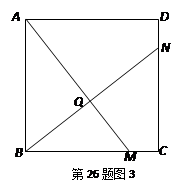

 经过点
经过点 和点P(t,0),且t≠0
和点P(t,0),且t≠0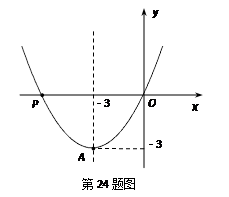
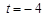 ,求a、b的值,并指出此时抛物线的开口方向
,求a、b的值,并指出此时抛物线的开口方向 粤公网安备 44130202000953号
粤公网安备 44130202000953号