（本小题满分14分）如图四棱锥P-ABCD中，底面ABCD是菱形，∠BAD＝60°，AD＝1，侧面PAD是正三角形，且与底面ABCD垂直，Q是AD的中点．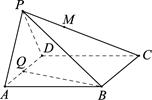
（1）求四棱锥P-ABCD的体积；
（2）M在线段PC上，PM＝tPC，问线段BC上是否存在一点R，使得当t∈(0，1)时，总有BQ∥平面MDR？若存在，确定R点位置；若不存在，请说明理由．
相关试题
（
，
为常数），且方程
有两个实根为
.
的解析式；
是定义在
上的减函数，并且满足
，
,
,
的值，（2）如果
，求x的取值范围。
,
，集合B=
。
=2时，求
； 
时，若元素
是
的必要条件，求实数
中，底面
为矩形，侧面
底面
，
，
．
；
与平面
所成的角为
， 
的余弦值．推荐套卷
（本小题满分14分）如图四棱锥P-ABCD中，底面ABCD是菱形，∠BAD＝60°，AD＝1，侧面PAD是正三角形，且与底面ABCD垂直，Q是AD的中点．
（1）求四棱锥P-ABCD的体积；
（2）M在线段PC上，PM＝tPC，问线段BC上是否存在一点R，使得当t∈(0，1)时，总有BQ∥平面MDR？若存在，确定R点位置；若不存在，请说明理由．
粤公网安备 44130202000953号