如图，在教学实践课中，小明为了测量学校旗杆CD的高度，在地面A处放置高度为1.5米的测角仪AB，测得旗杆顶端D的仰角为32°，AC=22米，求旗杆CD的高度．（结果精确到0.1米．参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）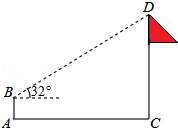
的过程如图。
；
≤
；
≤
﹣
=1的过程如图．请指出他解答过程中的错误，并写出正确的解答过程．
相关知识点
推荐套卷
如图，在教学实践课中，小明为了测量学校旗杆CD的高度，在地面A处放置高度为1.5米的测角仪AB，测得旗杆顶端D的仰角为32°，AC=22米，求旗杆CD的高度．（结果精确到0.1米．参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）
粤公网安备 44130202000953号