将油箱注满k升油后,轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=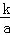 (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
相关知识点
推荐套卷
将油箱注满k升油后,轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=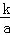 (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?