(本小题满分14分)给定数列 .对
.对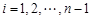 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后 项
项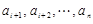 的最小值记为
的最小值记为 ,
,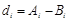 .
.
(Ⅰ)设数列 为
为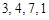 ,写出
,写出 ,
, ,
, 的值;
的值;
(Ⅱ)设 (
( )是公比大于
)是公比大于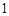 的等比数列,且
的等比数列,且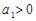 .证明:
.证明: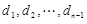 是等比数列;
是等比数列;
(Ⅲ)设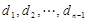 是公差大于
是公差大于 的等差数列,且
的等差数列,且 .证明:
.证明: 是等差数列.
是等差数列.
推荐套卷
(本小题满分14分)给定数列 .对
.对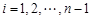 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后 项
项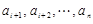 的最小值记为
的最小值记为 ,
,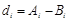 .
.
(Ⅰ)设数列 为
为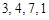 ,写出
,写出 ,
, ,
, 的值;
的值;
(Ⅱ)设 (
( )是公比大于
)是公比大于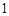 的等比数列,且
的等比数列,且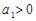 .证明:
.证明: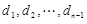 是等比数列;
是等比数列;
(Ⅲ)设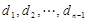 是公差大于
是公差大于 的等差数列,且
的等差数列,且 .证明:
.证明: 是等差数列.
是等差数列.