定义:若各项为正实数的数列 满足
满足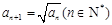 ,则称数列
,则称数列 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列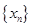 满足
满足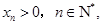 且
且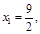 点
点 在二次函数
在二次函数 的图像上.
的图像上.
(1)试判断数列
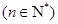 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记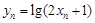
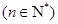 ,求证:数列
,求证:数列 是等比数列,并求出通项公式
是等比数列,并求出通项公式 ;
;
(3)从数列 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项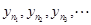 ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列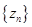 :
: .若数列
.若数列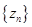 是首项为
是首项为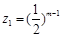 ,公比为
,公比为 的无穷等比数列,且数列
的无穷等比数列,且数列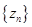 各项的和为
各项的和为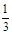 ,求正整数
,求正整数 的值.
的值.
相关知识点
推荐套卷
定义:若各项为正实数的数列 满足
满足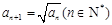 ,则称数列
,则称数列 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列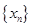 满足
满足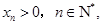 且
且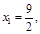 点
点 在二次函数
在二次函数 的图像上.
的图像上.
(1)试判断数列
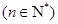 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记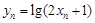
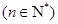 ,求证:数列
,求证:数列 是等比数列,并求出通项公式
是等比数列,并求出通项公式 ;
;
(3)从数列 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项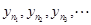 ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列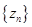 :
: .若数列
.若数列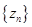 是首项为
是首项为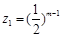 ,公比为
,公比为 的无穷等比数列,且数列
的无穷等比数列,且数列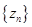 各项的和为
各项的和为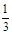 ,求正整数
,求正整数 的值.
的值.