某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶，每级小台阶都为0.4米．现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC（杆子的底端分别为D，C），且∠DAB=66°．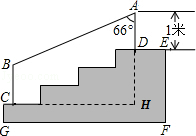
（1）求点D与点C的高度差DH的长度；
（2）求所用不锈钢材料的总长度l（即AD+AB+BC，结果精确到0.1米）．（参考数据：sin66°≈0.91，cos66°≈0.41，tan66°≈2.25，cot66°≈0.45）
相关试题
如图所示，已知△ABC的三个顶点的坐标分别为A（﹣2，3），B（﹣6，0），C（﹣1，0）．
（1）请直接写出点B关于点A对称的点的坐标；
（2）将△ABC绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点的坐标；
（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
如图，在▱ABCD中，点E是BC边的中点，连接AE并延长与DC的延长线交于F．
（1）求证：CF=CD；
（2）若AF平分∠BAD，连接DE，试判断DE与AF的位置关系，并说明理由．
满足x﹣y≤0，求k的最大整数值．
﹣1）÷
，再选择一个恰当的x值代入求值．
并把它的解集在数轴上表示出来．相关知识点
推荐套卷
粤公网安备 44130202000953号