将 绕点
绕点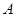 按逆时针方向旋转
按逆时针方向旋转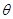 度,并使各边长变为原来的
度,并使各边长变为原来的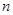 倍,得
倍,得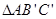 ,如图①,我们将这种变换记为
,如图①,我们将这种变换记为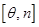 .
.
(1)如图①,对 作变换
作变换 得
得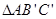 ,则
,则 ;直线
;直线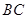 与直线
与直线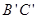 所夹的锐角为 度;
所夹的锐角为 度;
(2)如图②, 中,
中, ,
,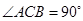 ,对
,对 作变换
作变换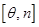 得
得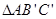 ,使点
,使点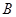 、
、 、
、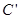 在同一直线上,且四边形
在同一直线上,且四边形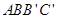 为矩形,求
为矩形,求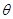 和
和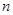 的值;
的值;
(3)如图③, 中,
中,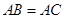 ,
, ,
,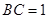 ,对
,对 作变换
作变换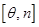 得
得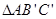 ,使点
,使点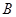 、
、 、
、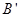 在同一直线上,且四边形
在同一直线上,且四边形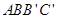 为平行四边形,求
为平行四边形,求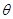 和
和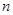 的值.
的值.
相关知识点
推荐套卷
将 绕点
绕点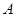 按逆时针方向旋转
按逆时针方向旋转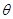 度,并使各边长变为原来的
度,并使各边长变为原来的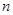 倍,得
倍,得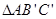 ,如图①,我们将这种变换记为
,如图①,我们将这种变换记为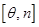 .
.
(1)如图①,对 作变换
作变换 得
得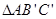 ,则
,则 ;直线
;直线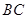 与直线
与直线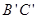 所夹的锐角为 度;
所夹的锐角为 度;
(2)如图②, 中,
中, ,
,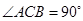 ,对
,对 作变换
作变换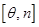 得
得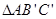 ,使点
,使点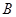 、
、 、
、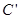 在同一直线上,且四边形
在同一直线上,且四边形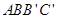 为矩形,求
为矩形,求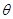 和
和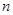 的值;
的值;
(3)如图③, 中,
中,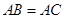 ,
, ,
,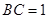 ,对
,对 作变换
作变换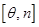 得
得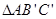 ,使点
,使点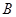 、
、 、
、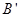 在同一直线上,且四边形
在同一直线上,且四边形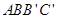 为平行四边形,求
为平行四边形,求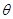 和
和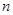 的值.
的值.