如图,甲船在港口P的南偏东60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度驶向港口P;乙船从港口P出发,沿南偏西45°方向驶离港口P.现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向,求乙船的航行距离(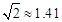 ,
, ,结果保留整数).
,结果保留整数).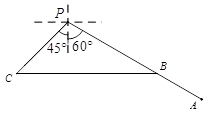
相关知识点
推荐套卷
如图,甲船在港口P的南偏东60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度驶向港口P;乙船从港口P出发,沿南偏西45°方向驶离港口P.现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向,求乙船的航行距离(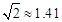 ,
, ,结果保留整数).
,结果保留整数).