（本小题满分12分）如图，在四棱台ABCD-A1B1C1D1中，DD1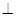
平面ABCD，底面ABCD是平行四边形，AB=AD=2A1B1,
（1）证明：BB1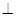AC；
（2）若AB=2，且二面角A1-AB-C大小为60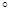
，连接AC,BD，设交点为O，连接B1O。求三棱锥B1-ABO外接球的体积。（球体体积公式：
,R是球半径）
相关试题
中，
、
、
的对边分别为
、
、
，若
（Ⅰ）求
、
，求三角形
求x的值；
，若
恒成立，求实数c的取值范围．
的图象的一条对称轴是直线
，
的值并写出
的解析式；
的图象经过怎样的变换可以得到
的图象？
的值；
求
的值．
，且
的值；（II）求
的值．推荐套卷
（本小题满分12分）如图，在四棱台ABCD-A1B1C1D1中，DD1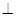平面ABCD，底面ABCD是平行四边形，AB=AD=2A1B1,
（1）证明：BB1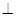AC；
（2）若AB=2，且二面角A1-AB-C大小为60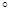，连接AC,BD，设交点为O，连接B1O。求三棱锥B1-ABO外接球的体积。（球体体积公式：,R是球半径）
粤公网安备 44130202000953号