已知椭圆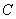 :
: 的离心率等于
的离心率等于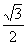 ,点
,点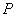
 在椭圆上.
在椭圆上.
(I)求椭圆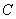 的方程;
的方程;
(Ⅱ)设椭圆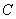 的左右顶点分别为
的左右顶点分别为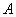 ,
, ,过点
,过点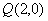 的动直线
的动直线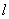 与椭圆
与椭圆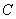 相交于
相交于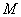 ,
,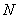 两点,是否存在定直线
两点,是否存在定直线 :
: ,使得
,使得 与
与 的交点
的交点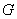 总在直线
总在直线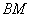 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的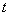 值;若不存在,说明理由。
值;若不存在,说明理由。
推荐套卷
已知椭圆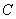 :
: 的离心率等于
的离心率等于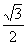 ,点
,点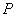
 在椭圆上.
在椭圆上.
(I)求椭圆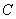 的方程;
的方程;
(Ⅱ)设椭圆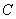 的左右顶点分别为
的左右顶点分别为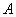 ,
, ,过点
,过点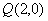 的动直线
的动直线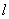 与椭圆
与椭圆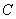 相交于
相交于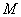 ,
,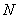 两点,是否存在定直线
两点,是否存在定直线 :
: ,使得
,使得 与
与 的交点
的交点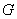 总在直线
总在直线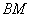 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的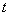 值;若不存在,说明理由。
值;若不存在,说明理由。