袋子 和
和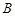 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从 中摸出一个红球的概率是
中摸出一个红球的概率是 ,从
,从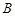 中摸出一个红球的概率为
中摸出一个红球的概率为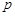 .
.
(1)从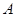 中有放回地摸球,每次摸出一个,共摸4次.
中有放回地摸球,每次摸出一个,共摸4次.
①恰好有2次摸到红球的概率;②第一次、第三次摸到红球的概率.
(2)若 、
、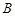 两个袋子中的球数之比为4,将
两个袋子中的球数之比为4,将 、
、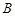 中的球装在一起后,从中摸出一个红球的概率是
中的球装在一起后,从中摸出一个红球的概率是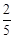 ,求
,求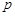 的值
的值
推荐套卷
袋子 和
和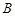 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从 中摸出一个红球的概率是
中摸出一个红球的概率是 ,从
,从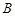 中摸出一个红球的概率为
中摸出一个红球的概率为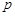 .
.
(1)从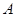 中有放回地摸球,每次摸出一个,共摸4次.
中有放回地摸球,每次摸出一个,共摸4次.
①恰好有2次摸到红球的概率;②第一次、第三次摸到红球的概率.
(2)若 、
、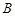 两个袋子中的球数之比为4,将
两个袋子中的球数之比为4,将 、
、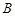 中的球装在一起后,从中摸出一个红球的概率是
中的球装在一起后,从中摸出一个红球的概率是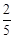 ,求
,求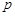 的值
的值