不透明的袋中有8张大小和形状完全相同的卡片,卡片上分别写有1,1,2,2,3,3,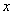 ,
,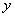 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
(I)求取出的三张卡片中至少有一张字母卡片的概率;
(Ⅱ)设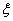 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时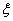 为这二个数字之和,否则
为这二个数字之和,否则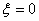 ,求
,求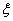 的分布列和期望
的分布列和期望 .
.
推荐套卷
不透明的袋中有8张大小和形状完全相同的卡片,卡片上分别写有1,1,2,2,3,3,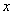 ,
,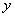 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
(I)求取出的三张卡片中至少有一张字母卡片的概率;
(Ⅱ)设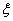 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时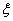 为这二个数字之和,否则
为这二个数字之和,否则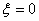 ,求
,求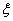 的分布列和期望
的分布列和期望 .
.